Statement I The ordinate of a point describing the circle x 2 y 2 = 25 decreases at the rate of 15 cm/s The rate of change of the abscissa of the point when ordinate equals 4 cm is 2 cm/s Statement II xdx ydy = 0 An object moves around x^2 y^2 = 25 (which represents a circle whose radius is 5 meters) at a constant speed At time t = 0 seconds, the object is at (5, 0) When t = 1, it is at (4, 3) Where is the object when t = 2? If tangents pq and pr are drawn from a point on the circle x^2 y^2 = 25 to the ellipse x^2/16y^2/b^2=1, (b

The Equation Of The Tangent To The Circle X 2 Y 2 25 Passing Thr
Radius of circle x^2+y^2=25
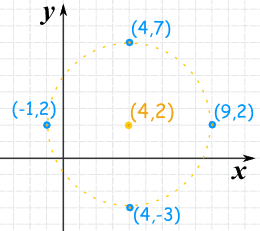
Radius of circle x^2+y^2=25-Circle Equations Level 1 Level 2 ExamStyle Description Help More Graphs This is level 2 equations of tangents to circles 1) Find the gradient of the radius of the circle x 2 y 2 = 10 that meets the circumference at (1,3) 2) Find the gradient of the tangent of the circle x 2 y 2 = 10 that touches the circle at (3,1) 3) One of theDoes the point (4, 2) lie inside or outside or on the circle x^2 y^2 = 25?




2 3 Equation Of A Circle How Is
1 In the accompanying diagram, the center of circle O is (0,0), and the coordinates of point P are (3,4) If OP is a radius, what is the equation of the circle?X^ {2}y^ {2}25=0 Subtract 25 from both sides x=\frac {0±\sqrt {0^ {2}4\left (y^ {2}25\right)}} {2} This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 0 for b, and 25y^ {2} for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} x=\frac {0±\sqrt {4\left (y^ {2}Circle x 2 y 2 = 25 Points of tangency (5 c o s θ, 5 s i n θ) {0 ≤ θ < 2 π} Tangent lines c o s θ x s i n θ y = 5
Question Solve by graphing x^2y^2=25 and x2y=5 I graphed my circle and line perfectly but when it came to using either addition or substitution methods to find the solution set (where the line crosses the circle at two points) I had problems( I can see by looking at my graph that one solution is (5,0) and the otherMay 08 When the polynomial x^4 bx^3 5x^2 dx 6 is divided by x 2 the remainder is 16 When it is divided by x 1 the remainder is 10 Find the value of constant d November 1994This lesson will cover a few examples to illustrate shortest distance between a circle and a point, a line or another circle Example 1 Find the shortest and the longest distance between the point (7, 7) and the circle x 2 y 2 – 6x – 8y 21 = 0 Solution We've established all the required formulas already in a previous lessonStill, have a look at what's going on
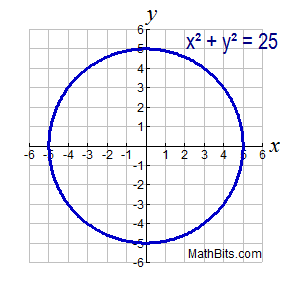
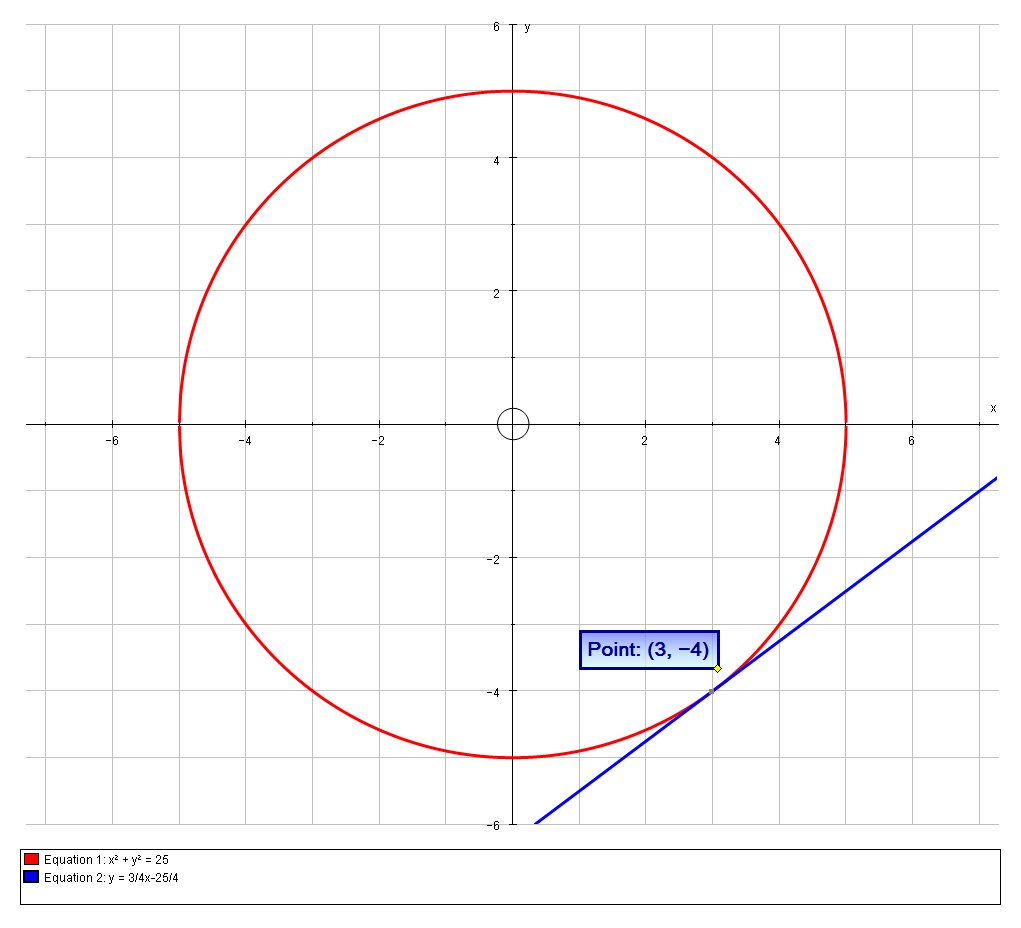
X^2y^2=1 radius\x^26x8yy^2=0 center\(x2)^2(y3)^2=16 area\x^2(y3)^2=16 circumference\(x4)^2(y2)^2=25 circleequationcalculator x^2y^2=1 enThe equation of the tangent to the circle x^2 y^2 = 25 at (3, 4) has to be determined without using calculus In a circle, the radius is perpendicular to the tangent at any pointAlgebra Graph x^2y^2=25 x2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the yoffset from



Graphing Quadratic Functions Mathbitsnotebook Ccss Math



Circle Equations
Maths AB is a chord of the circle x2 y2 = 25 The tangents to the circle at A and B intersect at C If (23) is the midpoint of AB, then the area of quadrilateral OACB (where O is origin) is A To C 50/31) x2 y2 =2 2) x 2y =4 3) x 2y =8 4) x2 y2 =16 3 What is anIn the given figure, the circle x^2 y^2 = 25 intersects the xaxis at thepoint A and B The line x = 11 intersects the xaxis at the point CPoint P moves along the line x = 11 above the xaxis and AP intersects the circle at Q Find Updated On To keep watching this video solution for




Question Video Finding The Center And Radius Of A Circle Using The Equation Of A Circle Nagwa




2 3 Equation Of A Circle How Is
May 1995 What is the radius of the circle x^2 y^2 6x = 0?Solution Z Z D e−x 2−y2 dA = Z π/2 −π/2 Z 2 0 e We have x2 y2 = 25 We should recognise this as a circle of radius 5 centred on the origin Differentiating Implicitly wrt x we get 2x 2y dy dx = 0 ∴ y dy dx = − x ∴ dy dx = − x y Nowe we differentiate a second time (implicitly) whilst applying the quotient rule d2y dx2 = − (y)(1) − (x)( dy dx) (y)2



How Do You Find An Equation For The Line Tangent To The Circle X 2 Y 2 25 At The Point 3 4 Socratic




How Do You Find An Equation For The Line Tangent To The Circle X2 Y2 25 At The Point 3 4 Brainly In
Type your response in the box Imagine that this graph represents the distance Brianna travels to get to her babysitting job with respect to time DesGiven the circle x^2 y^2=25 and point P (x1,y1)on the circle, find the equation of the line in slopeintercept form that is tangent to the circle at point P check_circleFree Circle Circumference calculator Calculate circle circumference given equation stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy circumference x^2y^2=1 en Related Symbolab blog posts My Notebook, the Symbolab way
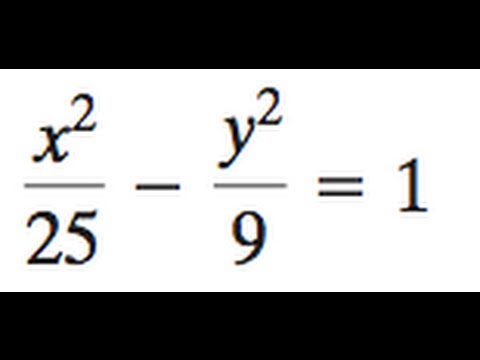



Hyperbola X 2 25 Y 2 9 1 Youtube



What Is The Radius Of The Circle S That Touches The Hyperbola X 2 Y 2 25 In Exactly Two Places And Touches The Circle X 2 Y 2 25 In One Quora
The second part just uses the formula (xa)^2=x^22axa^2 twice You are right about the first part The second part just uses the formula ( x a ) 2 = x 2 2 a x a 2 twiceCircle on a Graph Let us put a circle of radius 5 on a graph Now let's work out exactly where all the points are We make a rightangled triangle And then use Pythagoras x 2 y 2 = 5 2 There are an infinite number of those points, here are some examplesFor the circles to touch, we must show that they intersect at exactly one point We have the equations of the two circles x2 y2 = 25 x 2 y 2 = 2 5 and x2 y2 − 24x − 18y 125 = 0 x 2 y 2 − 2 4 x − 1 8 y 1 2 5 = 0 Substituting the first equation into the second (or alternatively subtracting the first equation from the




If The Circle X A 2 Y 2 25 Intersect The Circle X 2 Y B 2 16 In Such A Way That Com Youtube




Graph A Circle In Standard Form X 2 Y 2 2 25 Algebra Ia 08 01 Youtube
25 pi The center of the circle is at (0,0) and, when x = 0, the circle points are at y=5 and y=5 So, the radius of the circle is r = 5 The area of a circle is given by pi r^2 So, substituting r=5, one gets the answer 25 piLet P(3,4) be a point on the circle x 2 y 2 = 25 (a) What is the slope of the line joining P and O(0, 0)?Does the point (4, 2) lie inside or outside or on the circle x^2 y^2 = 25?




Solved Find The Slope Of The Tangent Line To The Circle X Chegg Com
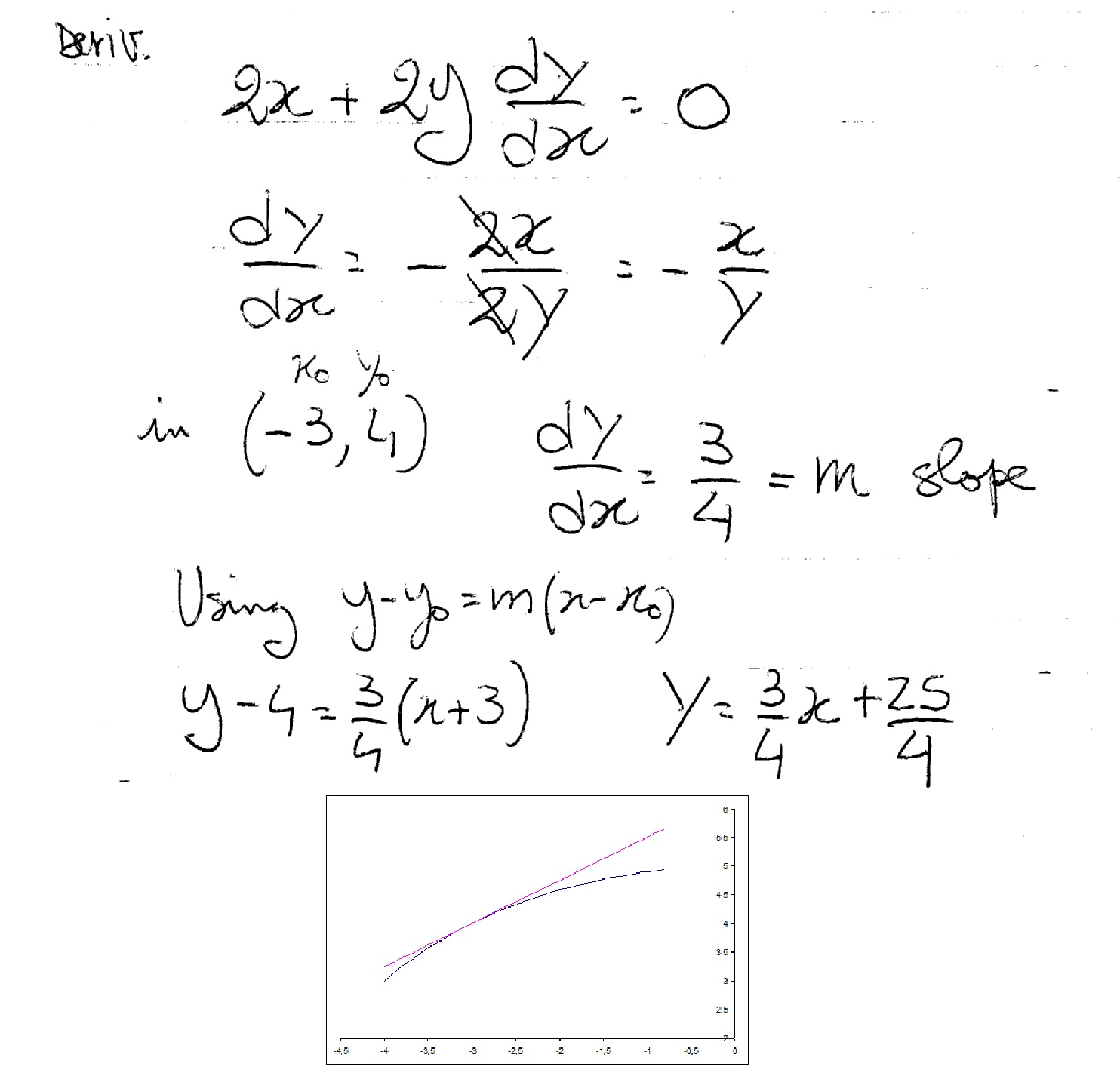



How Do You Find Equation Of Tangent To Circle X 2 Y 2 25 At The Point 3 4 Socratic
Solution for If x 2 y 2= 25 , find dy /dxR cos(x 2 y2)dA where R is the region that lies above the xaxis within the circle x2 y2 = 9;Show that the line $3x4y=25$ and the circle $x^2y^2=25$ intersect in two coincident points Mathematics Stack Exchange




Write The Standard Form Of The Equation For The Chegg Com



Geometry 10 6 Equations Of A Circle Ppt Download
An explanation on how to start would be helpful plz thxHyperbola hyperbola The equation of a circle whose center is at (1,2) and radius is 5 is (x 1)² (y 2)² = 5 (x 1)² (y 2)² = 25 (x 1)² (y 2)² = 25 (x 1)² (y 2)² = 25 Find the major intercepts for the ellipse x^2/4y^2/9=1 (±2, 0)By the symmetry of the circle, required area of the circle is 4 times the area of the region OPQO For the region OPQO, the limits of integration are x = 0 and x = 5 Given equation of the circle is x 2 y 2 = 25



View Question The Equation Of A Circle Is X 3 2 Y 5 2 25
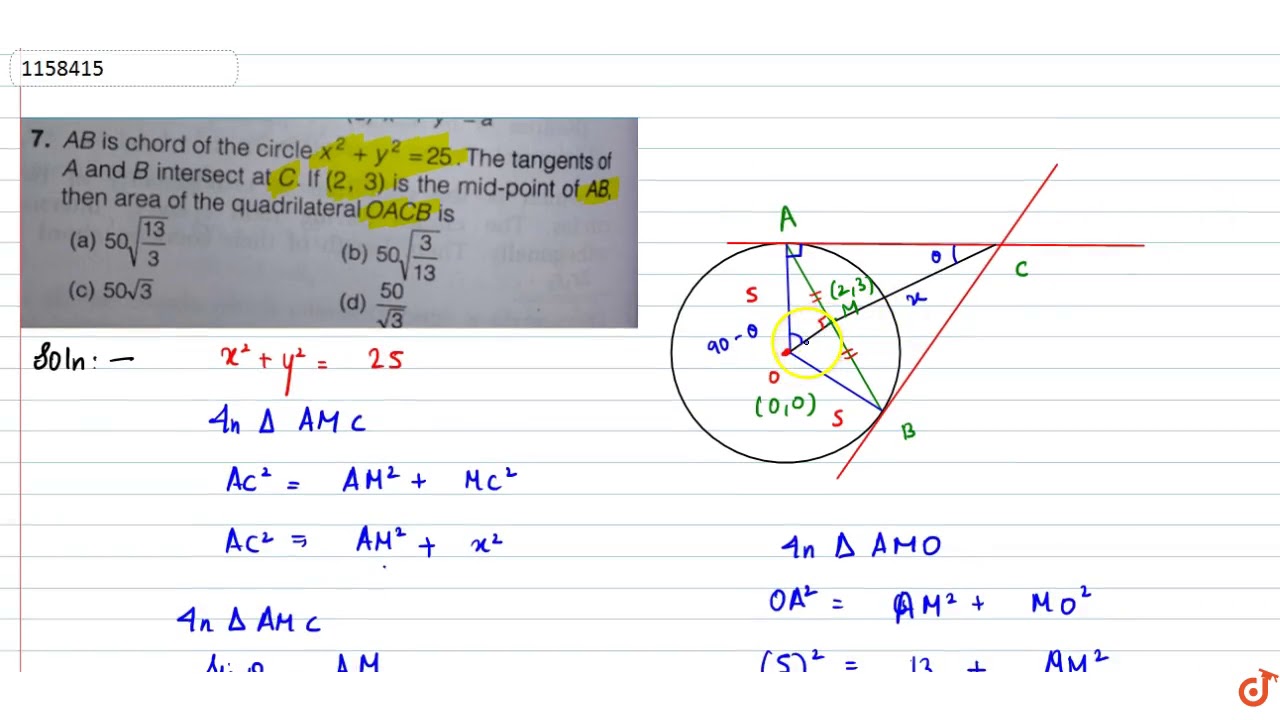



Ab Is A Chord Of The Circle X 2 Y 2 25 The Tangents Of A And B Intersect At C If 2 3 I Youtube
When t = n? Two lines PQ and PR are drawn from a point on the circle x 2 y 2 = 25 to the ellipse x 2 /4 2 y 2 /b 2 = 1 where b < 4 If the parallelogram PQSR is completed and S lies on the circumcircle of ΔPQR, then the eccentricity of ellipse is (a) √7/3AB is a chord of the circle `x^2 y^2=25` The tangents of A and B intersect at C If (2, 3) i If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the
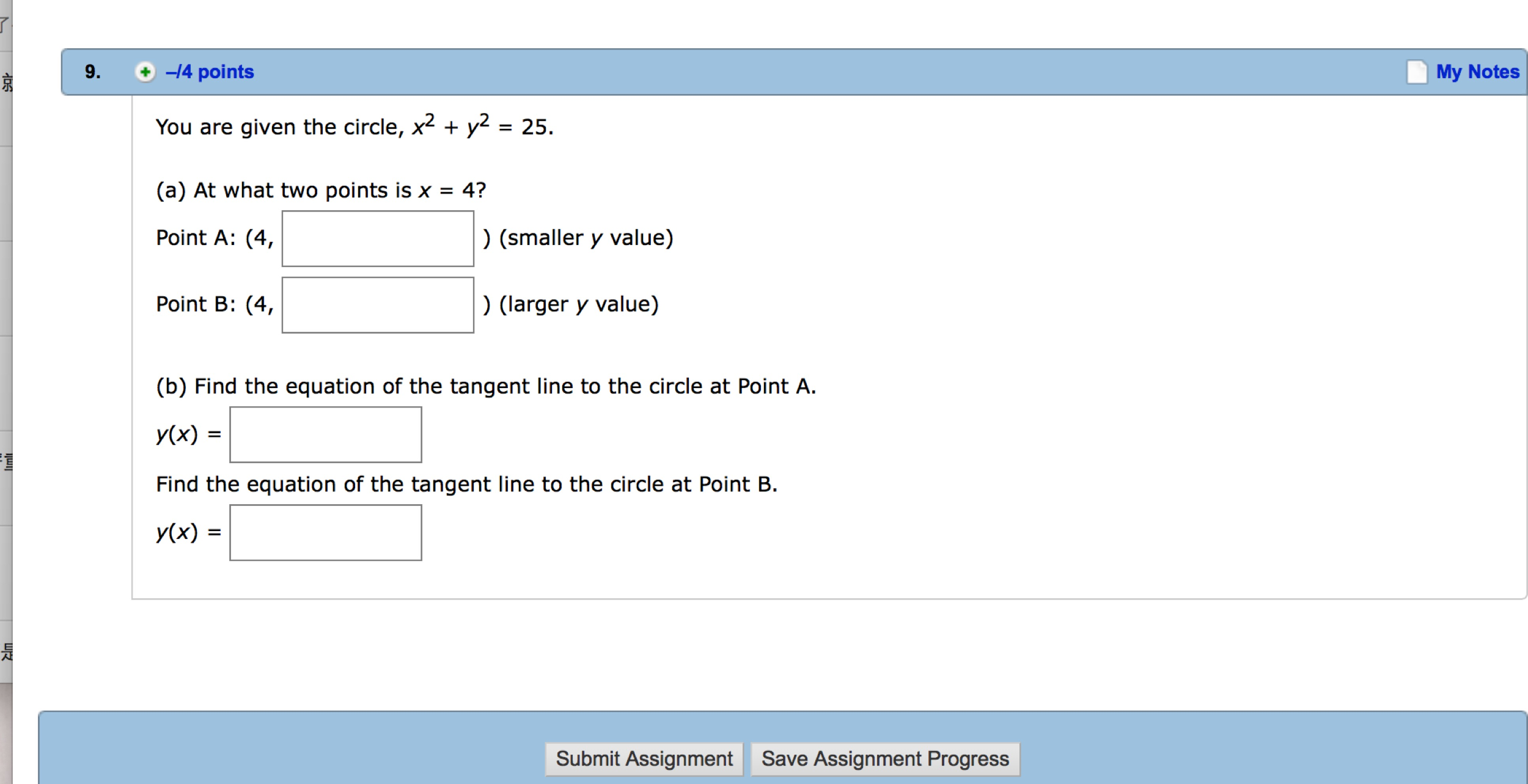



Solved You Are Given The Circle X 2 Y 2 25 A At W Chegg Com




Find The Center And Radius Of This Circle X Chegg Com
Type your response in the box Imagine that this graph represents the distance Brianna travels to get to her babysitting job with respect to time DesWhen t = 3?X^2 y^2 =25 is a circle centred at 0 and radius = 5 3x 4y = 25, one solution is x=3 and y = 4 which is 5 away from origin and is a point on the circle The coincidental point is (3,4)
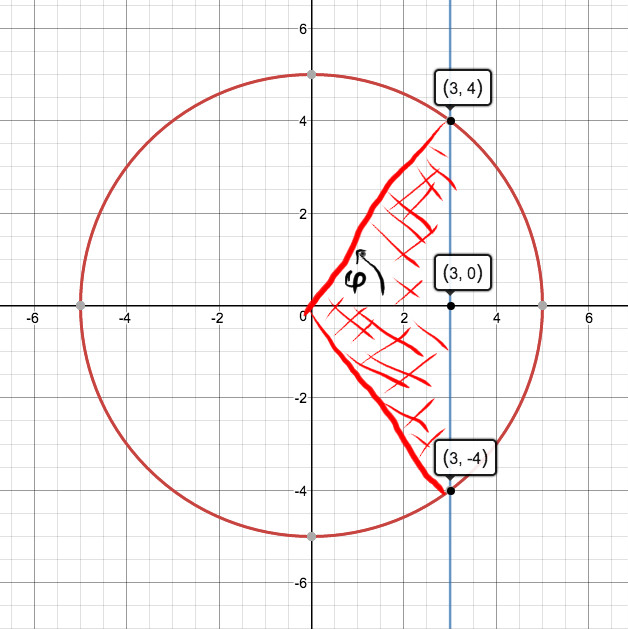



How Do You Write The Definite Integral To Find The Smaller Area Cut From The Circle X 2 Y 2 25 By The Line X 3 Socratic




Example 1 Find Area Enclosed By Circle X2 Y2 Examples
Does the point (4, 2) lie inside or outside or on the circle x^2 y^2 = 25?What is the equation of the normal to the curve x^2 y^2 = 25 at (4, 3)?1) x2 y2 =5 2) x 2y =9 3) x2 y2 =16 4) x2 y2 =25 2 What is an equation for the circle shown in the graph below?
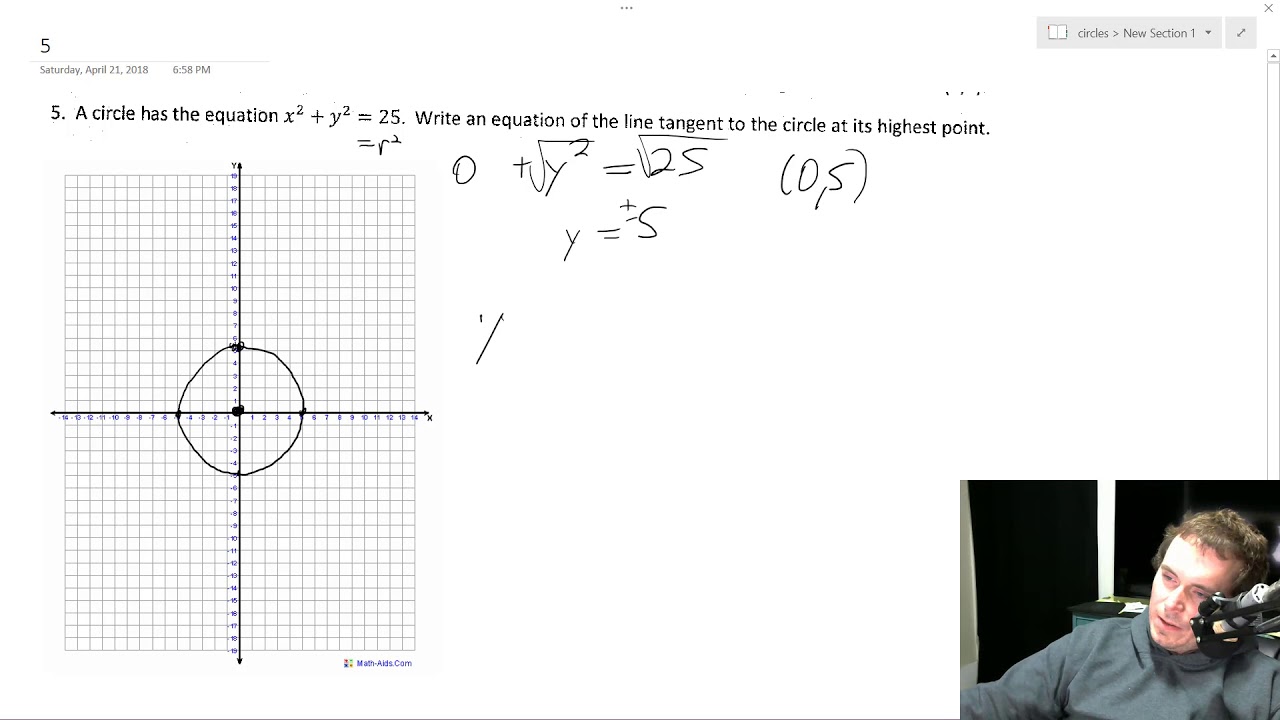



A Circle Has The Equation X 2 Y 2 25 Write An Equation Of The Line Tangent Youtube




The Differential Equation Of The Family Of Circles With Fixe
Find the volume of the solid whose base is the circle x^2y^2=25 and the cross sections perpendicular to the xaxis are triangles whose height and base are equal Find the area of the vertical cross section A at the level x=1(b) Find an equation of the tangent line to the circle at P (c) Let Q(x, y) be another point on the circle in the first quadrantFind the slope m x of the line joining P and Q in terms of x (d) Calculate How does this number relate to your answer in part (b)?SolutionShow Solution Comparing the equation x 2 y 2 = 25 with x 2 y 2 = a 2, we get, a 2 = 25 ∴ a = 5 ∴ centre is (0, 0) and radius = a = 5 Concept Different Forms of Equation of a Circle



View Question Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25




What Is The Tangent Through 7 1 For Circle X 2 Y 2 25 Quora
Determine the equations of the tangents to the circle \(x^{2} y^{2} = 25\), from the point \(G(7;1)\) outside the circle Draw a sketch Consider where the two tangents will touch the circleAnswer and Explanation The equation of the given circle is x2 y2 = 25 Differentiating both sides with respect to x using the power rule and the chain rule 2x 2yy ′ = 0Subtracting 2xDoes the point (4, 2) lie inside or outside or on the circle x^2 y^2 = 25?




Circles
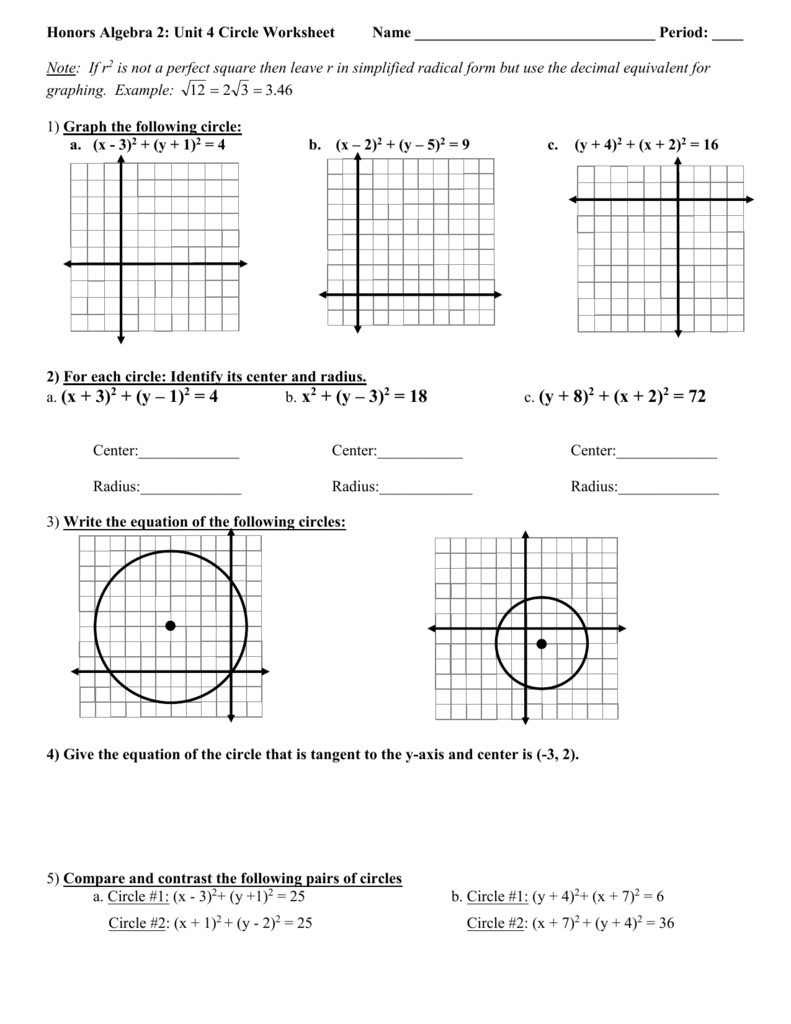



2
At what times does the object return to (5, 0)? What is the radius of curvature (3,4) on the circle x^2y^2=25 Get the answers you need, now!Vikram vikram Math Secondary School answered What is the radius of curvature (3,4) on the circle x^2y^2=25 1 See answer vikram is waiting for your help Add your answer and earn points




Geometry Mini Lesson Circle C Is Defined By The Equation X 4 2 2 Y 5 1 2 36 Which Of The Following Identifies The Center C H K And Radius Ppt Download
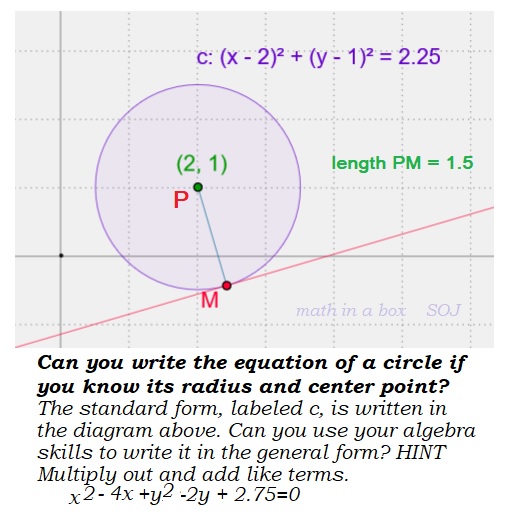



Circles In Algebra Math In A Box Lessons For Algebra Geometry And Precalculus
Use green's theorem to evaluate ∫c f·dr, where f(x,y) =< e^x x^2y , e^y xy^2 > and C is the circle x^2 y^2 = 25 oriented clockwise Expert Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculatorWhat is the object's speed?AB is a chord of the circle `x^2 y^2 = 25/2` P is a point such that PA = 4, PB = 3 If AB If playback doesn't begin shortly, try restarting your device Videos you watch may be added to the



What Is The Length Of The Chord Of The Circle X Y 25 Along The Line 3x 4y 15 0 Quora




The Equation Of The Tangent To The Circle X 2 Y 2 25 Passing Thr
This lesson will cover a few examples to illustrate the equation of the tangent to a circle in point formLet's begin Example 1 Find the equation of the tangent to the circle x 2 y 2 = 25, at the point (4, 3) Solution Note that the problem asks you to find the equation of the tangent at a given point, unlike in a previous situation, where we found the tangents of a given slopeSolution Prove that the line y = mx c y = m x c will touch the circle x2 y2 = 25 x 2 y 2 = 2 5 if c2 = 25(1 m2) c 2 = 2 5 ( 1 m 2) For the line to touch the circle there must be exactly one point of intersection between them—the line must be a tangent to the circleThe line from the center of the circle to the midpoint of a chord is perpendicular to the chord The center of the circle x2 y2 = 25 is (0,0) And the slope



Solution Stuck On How To Solve This Simultaneous Equation X 2 Y 2 25 X Y 7 Asap Please Thank You



Differential And Integral Calculus To The Circle X 4 2 Y 3 2 25 At The Point 7 1 7 Find The Equations Of The Tangents To The Hyperbola4x2 Gy2 36
Solution Z Z R cos(x2 y2)dA = Z π 0 Z 3 0 cos(r2)rdrdθ = (Z π 0 dθ)(Z 3 0 rcos(r2)dr) = π 2 sin9 (d) R R D e −x2−y2 dA where D is the region bounded by the semicircle x = p 4−y2;A variable straight line AB divides the circumference of the circle x 2 y 2 = 25 in the ratio 1 2 If a tangent CD is drawn to the smaller arc parallel to ABGiven Data {eq}\begin{align} \text{Circle } ~~x^2 y^2 &= 25\\\ \text{Line } ~~ 3x y &= 15\\ \end{align} {/eq} Solution {eq}\begin{align} 3x y &= 15




Which Of The Following Is A Result Of Shifting A Circle With Equation X 2 2 Y 3 2 25 To The Left 2 Brainly Com



Www Npsk12 Com Cms Lib Va Centricity Domain 37 Geometry Pdf
Find the Center and Radius x^2y^2=25 x2 y2 = 25 x 2 y 2 = 25 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k k represents the y




Circles Lesson 13 6 Describe What Each Of




Equation Of Tangent Line To Circle X 2 Y 2 100 At Point 6 8 Youtube




Does The Point 2 5 3 5 Lie Inside Outside Or On The Circle X 2 Y 2 25 Snapsolve




The Triangle Pqr Is Inscribed In The Circle X 2 Y 2 25 If Q And R Have Coordinates 3 4 And 4 3 Respectively Then Qpr Is Equal To



1
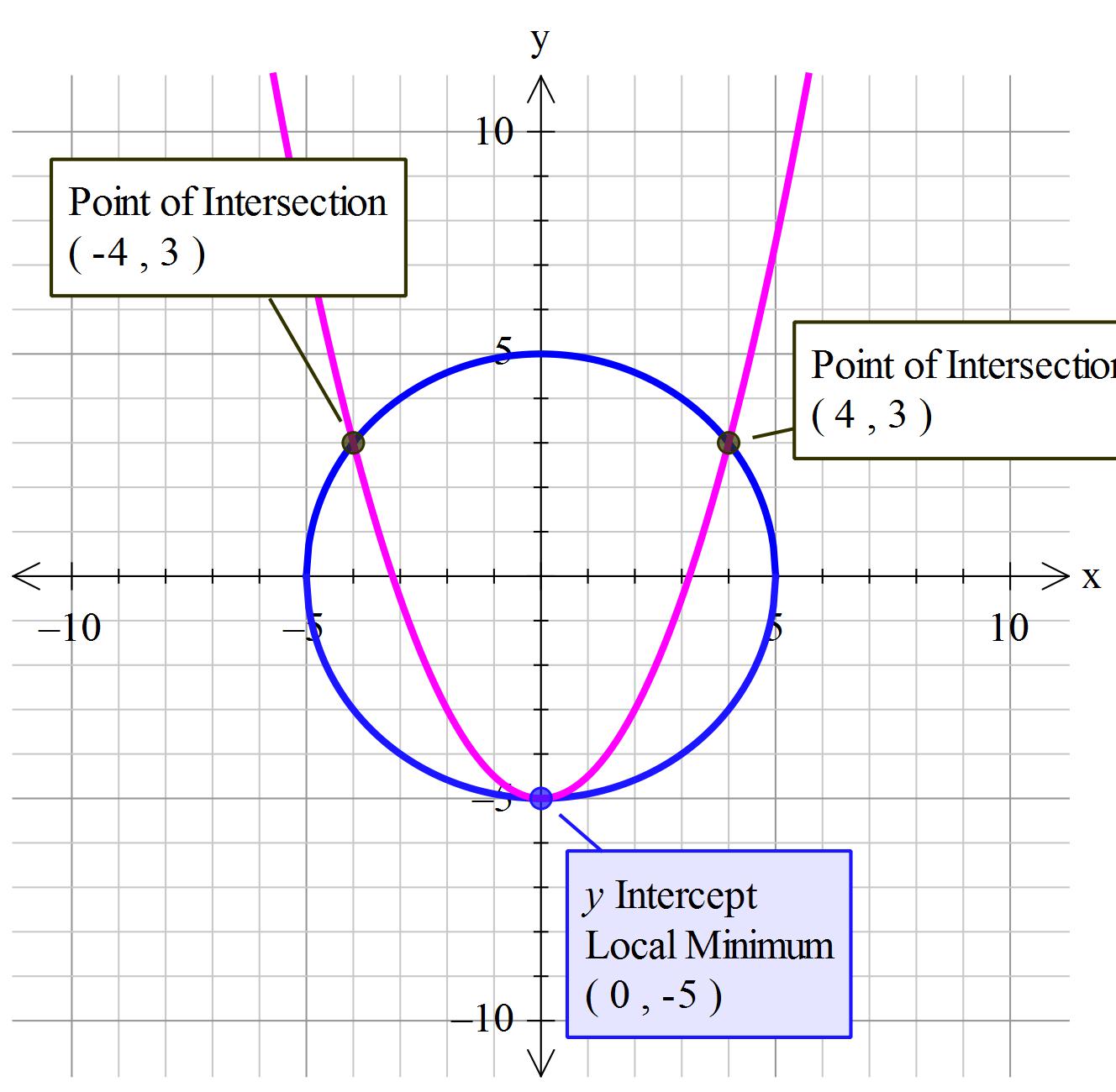



How Do You Solve X 2 Y 2 25 And Y 5 1 2x 2 Using Substitution Socratic




The Two Lines Through 2 3 From Which The Circle X2 Y2 25 Intercepts Chords Of Length 8 Maths Conic Sections Meritnation Com




X 6 2 Y 3 2 25 The Graph In The Xy Plane Of




Please Help Urgent Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25 Brainly Com




Convert The Rectangular Equation To Polar Form And Select Its Graph X 2 Y 2 25 Study Com




The Centre And Radius Of The Circle X 2 Y 2 25 Is



Solution Hi Can I Have Some Help With Finding This Function Find A Function Whose Graph Is The Bottom Half Of The Circle X 2 Y 2 25 F X




Once Again Consider The Circle With Equation X 2 Gauthmath



Solution Sketch The Graph Of X 2 2 Y 3 2 25



Solution X2 Y2 25 Is Solving This Problem Considered A Function How Do I Plot A Graph Using A Smooth Curve For This Problem Ed



Graphing A Circle Help Mathskey Com



Http Www Standrewspaisley Com Uploads 6 0 2 3 Circle Pupil Booklet Pdf



Solved Identify The Center And Radius Of The Circle With The Equation X 5 2 Y 12 2 25 Center Radius 2 Identify Course Hero



Search Q Equation Of A Circle Tbm Isch
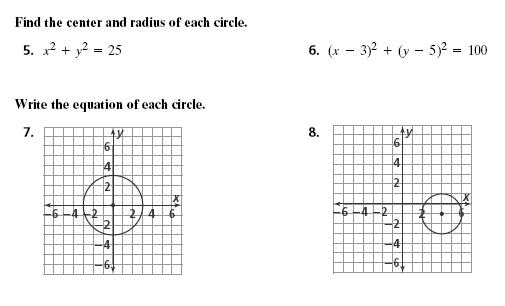



Find The Center And Radius Of Each Circle X2 Y2 Chegg Com



Graph X 2 Ky 2 25 For Different Values Of K
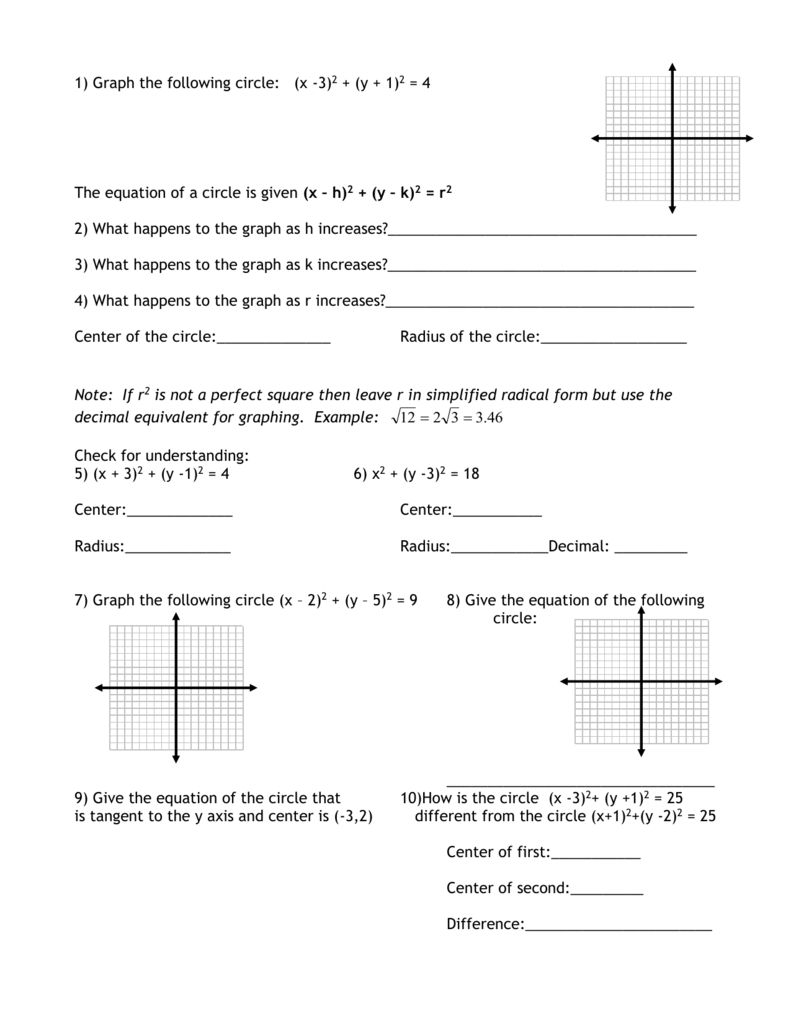



1 Graph The Following Circle X




10 What Is The Equation Of The Circle Represented By Chegg Com



Two Circles Have The Following Equations X 1 2 Y 4 2 25 And X 3 2 Y 3 2 49 Does One Circle Contain The Other If Not What Is The Greatest




Consider The Following C Counterclockwise Around Chegg Com




Which Graph Shows The Graph Of A Circle With Equation X 2 Y 4 2 16 Brainly Com
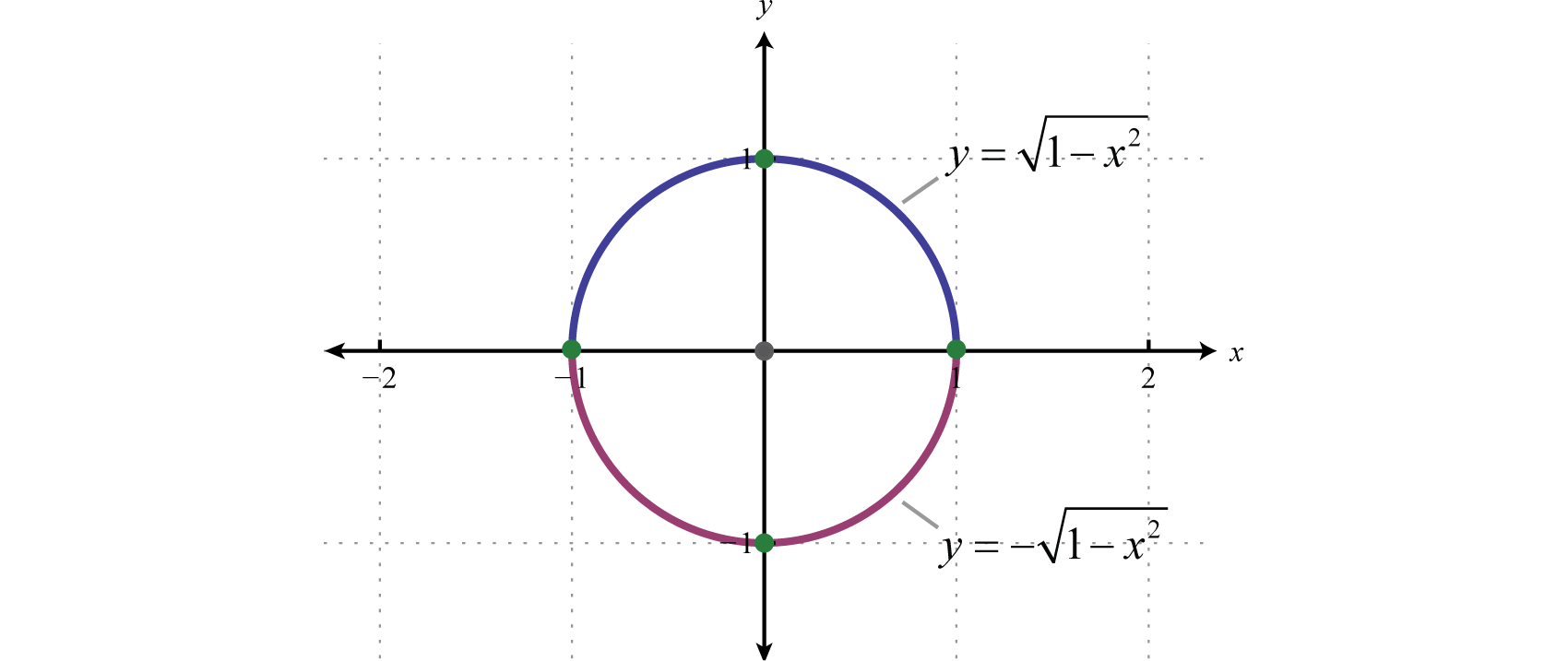



Circles




Find The Centre And Radius Of The Circle 2 X 1 2 2y 2 25 Brainly In




1 For Each Circle Equation Shown Below State The Chegg Com



Q Tbn And9gcqrtmhgysaakscrw Nolvz3a1qpo2sb Gorfekohspslxj99rif Usqp Cau




Show That The Tangent Of The Circle X 2 Y 2 25 At The Point 3 4 And 4 3 Are Perpendicul Youtube




Equation Of Tangent Line On Circle X 1 2 Y 2 2 25 Youtube
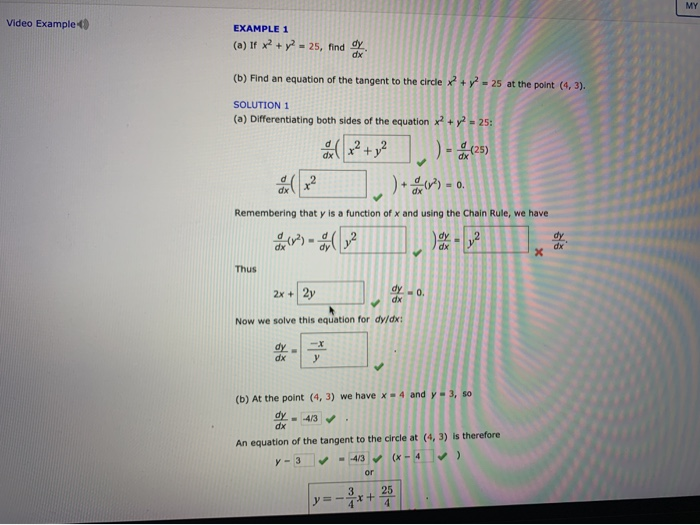



Video Example Example 1 A If X2 Y2 25 Find Y Chegg Com




2 1 R 2 16 R 0 0 R 2 25 R Special Pythagorean Triple Ppt Download



Www Npsk12 Com Cms Lib Va Centricity Domain 37 Geometry Pdf




Which Circle Corresponds To The Equation X 4 2 Y 4 2 25 Brainly Com




Solved The Equation X 1 2 Y 6 2 25 Describes A Circ Chegg Com




Example 1 A If X2 Y2 25 Find Dy Dx B Find An Chegg Com
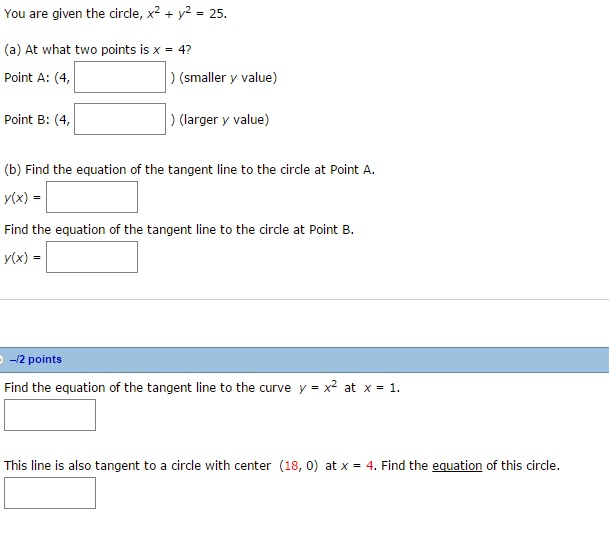



Solved You Are Given The Circle X 2 Y 2 25 At What Chegg Com



Solution Solve The Following System X2 Y 2 25 2x Y 10 The Solution Set




How Do You Find A Polar Equation For The Circle With Rectangular Equation X 2 Y 2 25 Homeworklib



What Is The Equation Of The Chord Of The Circle X 2 Y 2 25 Of Length 8 That Passes Through The Point 2 3 2 And Makes An Acute Angle With Positive X Axis Quora
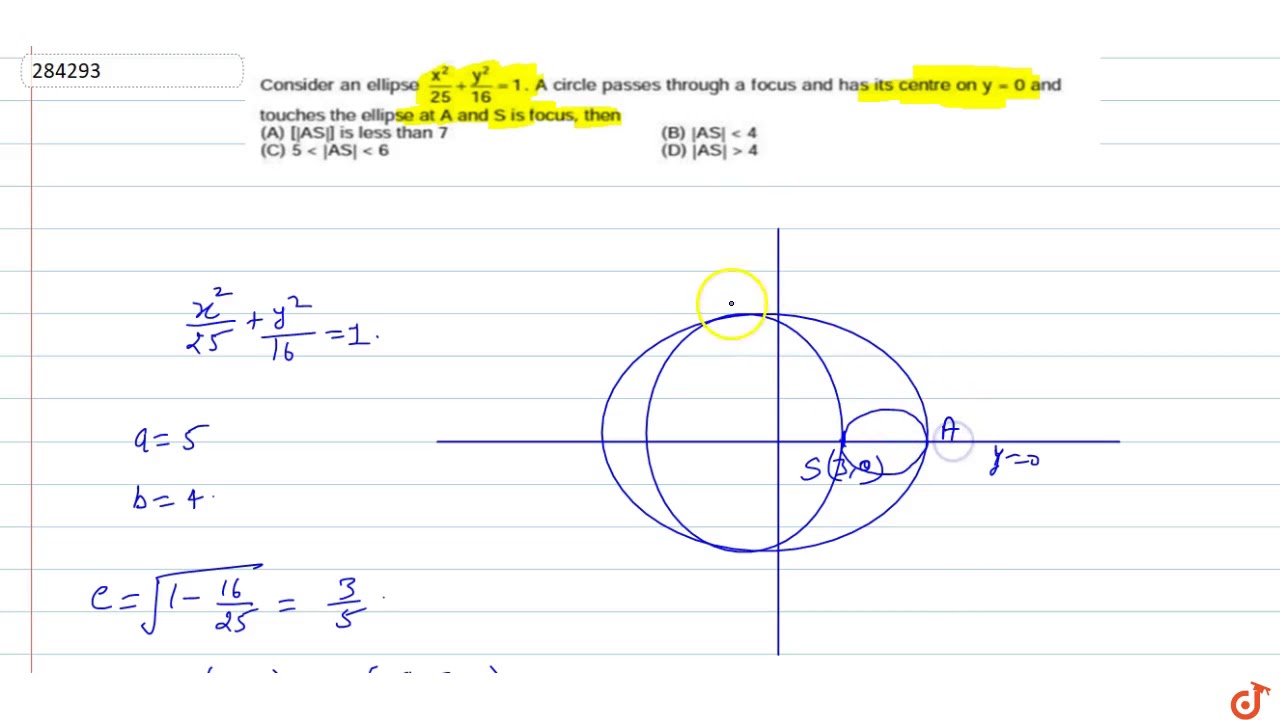



Consider An Ellipse X 2 25 Y 2 16 1 A Circle Passes Through A Focus And Has Its Centre On Youtube



Http Www Nicolet K12 Wi Us Faculty Dgibbon Circle ellipse answer sheet pdf Pdf




Implicit Differentiation




Inverse Of Relations Circles X 2 2 Y 2 25 And Ellipse Youtube
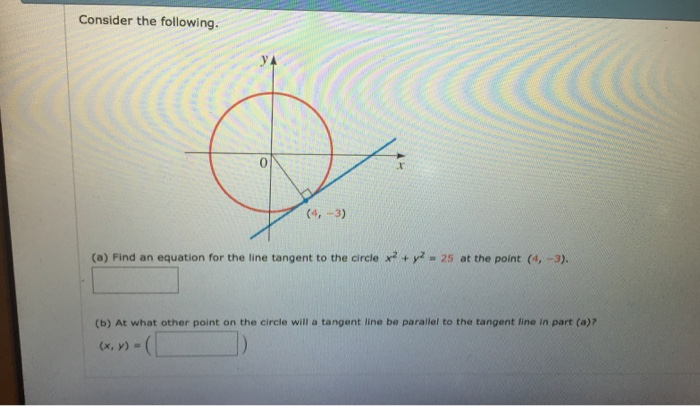



Consider The Following Find An Equation For The Chegg Com



Tangent Line Let P 3 4 Be A Point On The Circle X 2 Y 2 25 See Figure A What Is The Slope Of The Line




If The Circle X A 2 Y 2 25 Intersect The Circle X 2 Y B




If X 2 2 Y 5 2 25 Is The Equation Of A Circle Which Statement Describes The Circle S Brainly Com




Ab Is A Chord Of The Circle X 2 Y 2 25 2 P Is A Point Su
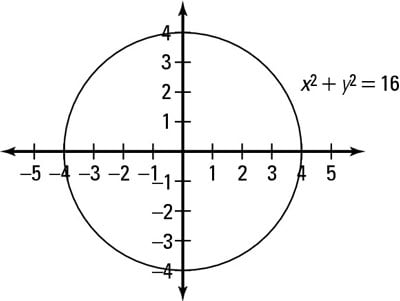



2 Ways To Graph A Circle Dummies
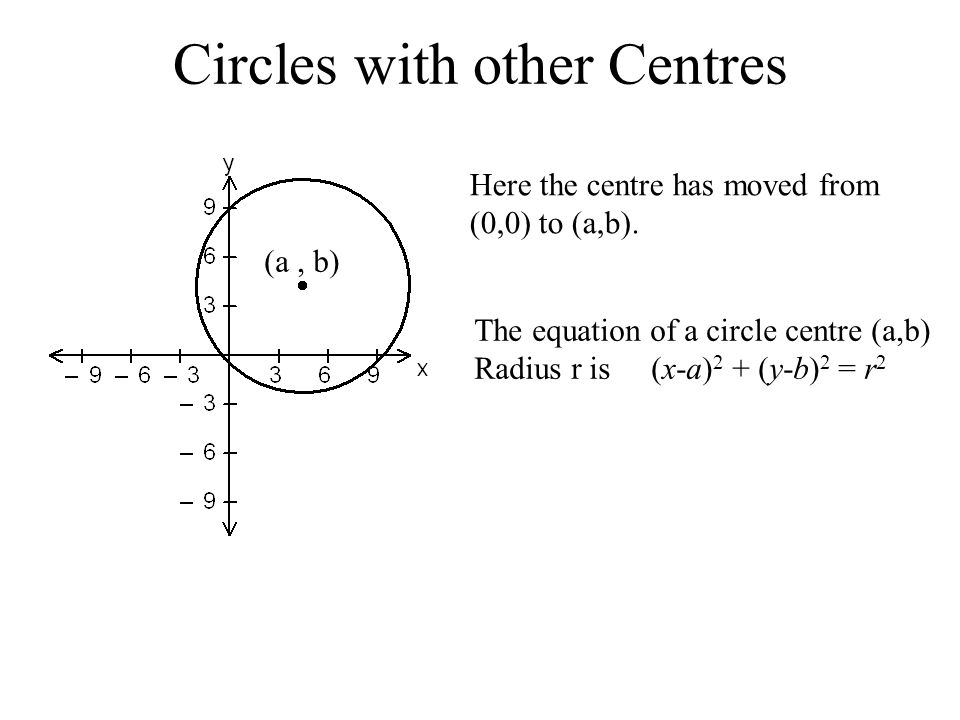



The Circle X 1 Y 1 X 2 Y 2 If We Rotate This Line We Will Get A Circle Whose Radius Is The Length Of The Line Ppt Download



Www Npsk12 Com Cms Lib Va Centricity Domain 37 Geometry Pdf




What Is The Center Of The Circle Represented By This Equation X2 Y 9 2 25 Brainly Com



4 2 Implicit Differentiation




The Equations Of The Tangents To The Circle X 2 Y 2 25 With Slop
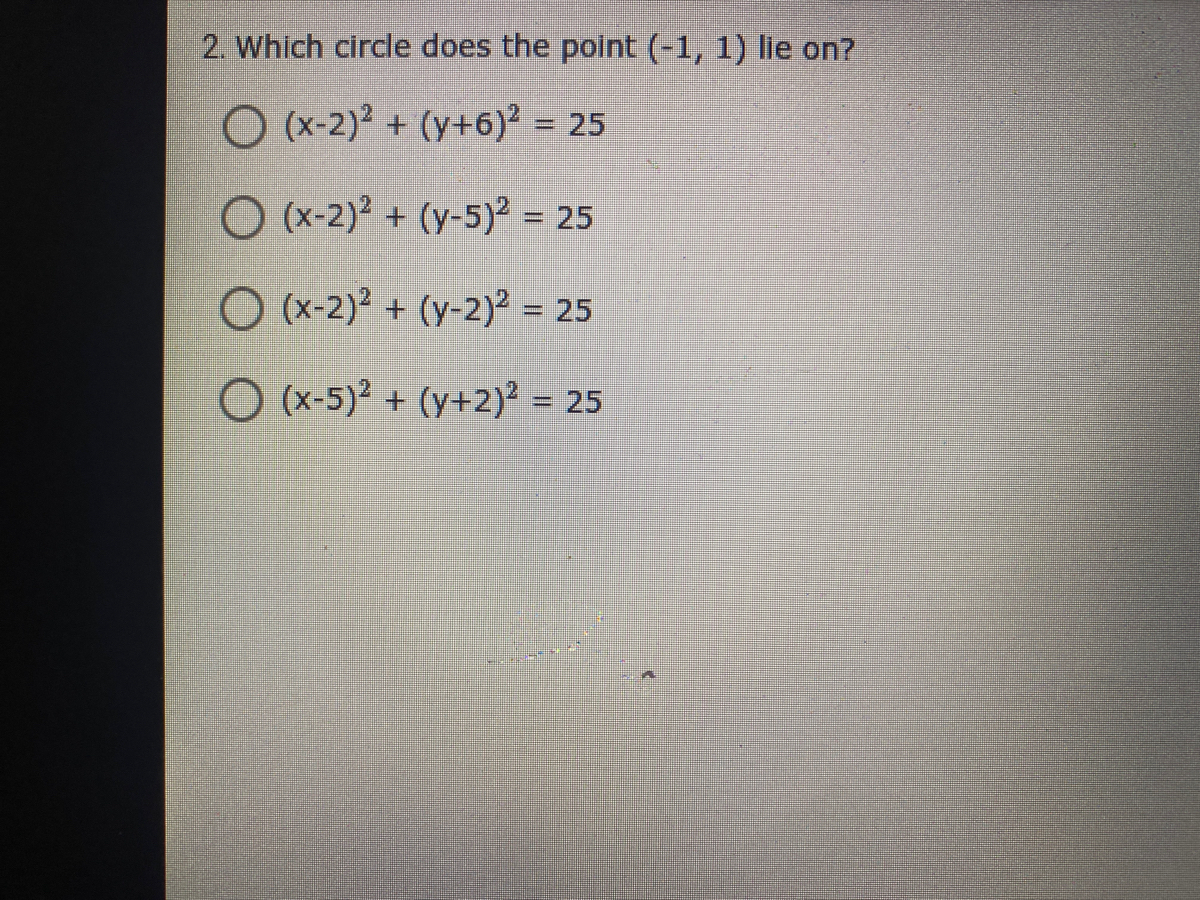



Answered 2 Which Circle Does The Point 1 1 Bartleby




Graph The Circle X 4 2 Y 2 2 25 Label The Center And At Least Four Points In The Circle Study Com




13 6 Circles T127 Circle Equation X H 2 Y K 2 R 2 Where H K Is The Center Of The Circle And R Radius Ppt Download



How Do You Solve The System X 2y 1 And X 2 Y 2 25 By Graphing Socratic




View Question Which Graph Shows The Graph Of A Circle With Equation X2 Y 5 2 25




Find The Point Of A Intersection Of Circle X 2 Y 2 25 And Line 4x 3y 12 And Also Find Length Of Intersecting Chord



Solution How Do You Graph X 4 Y 2 25 What Is The Area Of The Enclosed Region
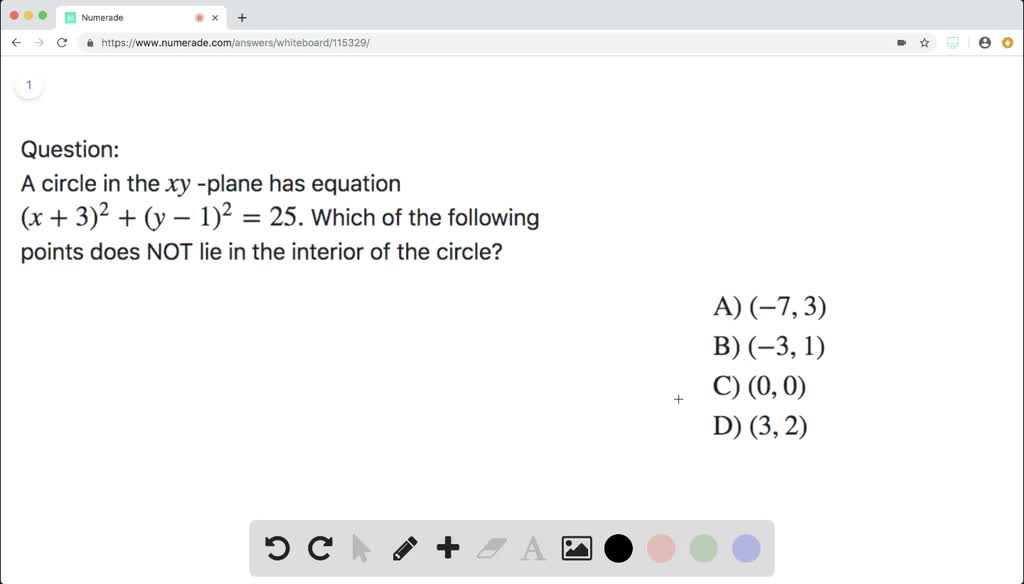



Solved A Circle In The X Y Plane Has Equation X




Find The Equation Of The Tangent To The Circle X 2 Y 2 25 Which Is Inclined At 60 Angle Youtube



Solution Sketch The Graph Of The Circle X 2 Y 2 2 25 Find The Circumference And The Area Of The Circle
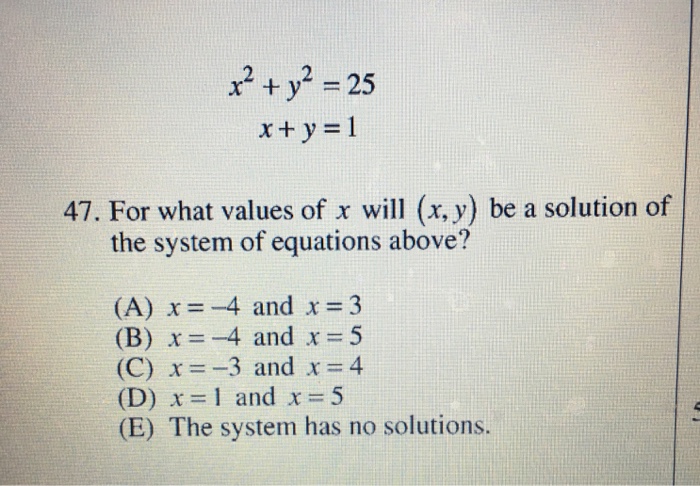



X 2 Y 2 25 X Y 1 For What Values Of X Will Chegg Com



1




The Equation Of A Circle Is X 2 Y 2 25 The Equation Of Its Cho



0 件のコメント:
コメントを投稿